Goals and Background:
The main goal of this lab exercise is to develop skills in performing key photogrammetric tasks on aerial photos and satellite images. Specifically, the lab is designed to aid in understanding the mathematics behind the calculation of photographic scales, measurements of areas and perimeters of features, and calculating relief displacement. Moreover, this lab is intended as an introduction to stereoscopy and performing orthorectification on satellite images. At the end of this lab exercise, students will be in a position to perform diverse photogrammetric tasks.
Methods
Scales Measurements and Relief Displacement
Calculating scale of nearly vertical aerial photographs
Although it may seem simple, it is extremely important to calculate real world distances on imagery. This gives more context as to the relationship between features and the imagery itself. Calculations can be done in multiple ways. One calculation is using the distance on the photo as well as the real world distance between points. The calculation can be seen below.
S= pd/gd
Where:
S = scale
pd = photo distance
gd = ground distance
The initial equation was
S = 2.7" / 8822.47'. 2.7" is the distance from point A to point B on the image and 8822.47' is the real world ground distance (which was provided by Dr. Cyril Wilson). A calculation was required to convert the feet to inches to be in the same units. This produced the converted equation:
2.7" / 105,869.64". In order to produce the equation in the form of scale, the numerator needed to become '1' so the numerator and denominator were divided by 2.4". This produced the equation
(2.7" / 2.7") / (105,869.64" /2.7") which gives us the scale of
1: 39,210.97 (figure 1).
 |
| Figure 1. The image used to find the distance between point A and point B. The actual scale of the imagery was found to be 1:39,210.97 which was found by using the real world ground distance as well as the distance on the image. |
Sometimes it is not possible to have a real world distance provided for a calculation, so a different equation can be used. This equation requires the person doing the calculations to know the focal lens length of the camera used to shoot the imagery as well as the altitude above sea level (ASL)and elevation of the terrain. The focal lens length for this image is 152 mm, the ASL is 20,000 feet, and the elevation of terrain is 796 feet. Below is the equation that was used:
S = f/ (H-h)
Where:
S = scale
f = focal lens length
H = altitude above sea level (ASL)
h = elevation of terrain
The initial equation (with numbers plugged in) was
152 mm / (20,000' -796'). Again, there needed to be a conversion done, so the feet in the denominator were converted to mm. That resulted in the equation
153 mm / 5853379.2 mm. The numerator needed to be '1' again in order to obtain the scale of the imagery. The equation was then
(152 mm / 152 mm) / (5853379.2 / 152) which resulted in the scale of
1: 38509.
Measurement of areas of features on aerial photographs
In addition to using the above methods to determine scale. Individual features can also be determined by using the measurement tool in ERDAS Imagine. The area the user wants to measure can be digitized using with the polygon shape.In the case of this lab, a lake was digitized, which can be seen below (figure 2). After 'closing' the shape, a perimeter and area appear at the bottom of the imagery (figure 3).
 |
| Figure 2. In order to determine the perimeter and area of the lake, the measurement tool was used to digitize a polygon around the edge of the water body. |
 |
| Figure 3. Perimeter and area displayed after digitizing the lake in figure _. |
The principal point is the optical center of an aerial photo.
To calculate relief displacement, the following equation must be used:
D = (h * r)/ H
Where:
D = relief displacement
h = height of object (real world)
r = radial distance of top of displaced object from principal point (photo)
H = height of camera above local datum
Calculating relief displacement from object height
Relief displacement is the displacement of objects and features on an aerial photograph from their true planimetric location on the ground. All objects above and below the found in all uncorrected imagery. All points collected away from the principal point will have some distortion because the imagery is being collected at an angle (figure 4).
 |
| Figure 4. Every feature collected from the sensor, except the point taken at the principal point has some displacement. This distorts how the image appears on the imagery. The above graphic illustrates how features are displaced at box 'A'. The feature appears to be leaning toward the principal point. |
Below is a real world example taken in Eau Claire of imagery with relief displacement (figure 5).
 |
| Figure 5. The principal point is located at the top left portion of the imagery. Notice the tower, indicated in the upper right portion of the imager. If there was no displacement you would not see the side profile of the tower, rather, it would appear as a circle (which would just show the top). |
Below is an example of the relief displaced tower (left) and the corrected tower (right) (figure 6).
 |
| Figure 6. Note the difference between the towers in the images. The one of the left's side profile can be seen where as the tower in the right image only appears as a circle, indicating that the right image's relief displacement has been corrected. |
Stereoscopy
Anaglyphs are stereoscopic photos that contain two images that overlap and are printed in different colors. With 3D glasses (that contain a red and blue filter in their respective lenses), anaglyphs appear to be 3D. Anaglyphs can be used in remote sensing to better understand to topography of an area.
Creation of anaglyph image with the use of a digital elevation model (DEM)
To create an anaglyph, the
Terrain tab was activated and the
Anaglyph button was pressed. From here, a DEM and regular aerial imagery were applied to the inputs. The exaggeration for this anaglyph was 1, which means that no exaggeration was applied to the image. The output image for this is seen in the results section (figure 12).
Creation of anaglyph image with the use of a LiDAR derived surface model (DSM)
Similar to the above anaglyph creation with the DEM, a DSM anaglyph was also generated. Figure _ below illustrates the DSM anaglyph next to the DSM imagery from which the output anaglyph was derived. The areas that 'pop' the most on the DSM imagery are the locations where there are changes in the DSM (figure 7). The output image for this is seen in the results section (figure 13).
 |
| Figure 7. Digital surface model (DSM) (left) in comparison to the ec_quad anaglyph (right). |
Orthorectification
Orthorectification is a complicated process whose purpose is to simultaneously remove positional and elevation errors from one or more aerial photos or satellite image scenes. This involves obtaining real world x,y, and z coordinates of pixels for aerial photos and images. Ultimately these images can be used to create orthophotos, stereopairs, and DEMs to name a few. Important elements of orthorectification include the pixel coordinate system, image coordinate system, image space coordinate system, and ground coordinate system.
This section of the lab, we will utilize the ERDAS Image Lecia Photogrammetric Suite (LPS) which is used in digital photgrammetry for triangulation, orthorectification of images collected by various sensors, extraction of digital surface and elevation models etc. A planimetrically true orthoimage will be created using LPS in this section.
A New Block File was created in the Imagine Photogrammetry Project Manager window. The Polynomial-based Pushbroom was selected as the geometric model. The projections for the horizontal and vertical reference coordinate system were set to UTM, the Clarke 1866 spheroid was chosen, and NAD27(CONTUS) was chose as the datum. The parameters of the SPOT Pushbroom were then established to enable the next step of the orthorectification process (although the default parameters were used).
The point measurement tool was activated (specifically the
Classic Point Measurement tool)
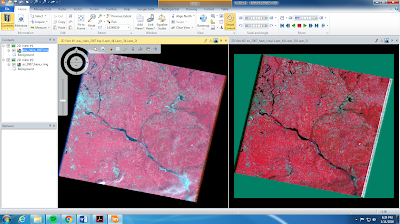
and the GCPs could then be collected. The GCP locations were based on the locations provided by Dr. Cyril Wilson (figure 8). After 2 points were collected, the
Automatic (x,y) Drive icon could be utilized. This feature can only be used after 2 GCPs are established. This feature speeds up the process of collecting GCPs, which was highly appreciated during this marathon lab. 9 GCPs were collected in total. The last two GCPs were collected using
NAPP_2m-ortho.img. The spatial resolution of the orthoimage was 2 meters. The GCPs were collected on the point measurement box, which could be viewed after the GCPs were collected (figure 9).
 |
| Figure 8. Process of GCPs being collected for orthorectification. The reference image is on the left and the uncorrected image is on the right. |
 |
| Figure 9. Point measurement box which indicates the GCP points collected on the imagery. |
In addition to a horizontal reference, a vertical reference needed to be established used a DEM. A DEM was selected as the reference and the z values were selected to establish the z values.
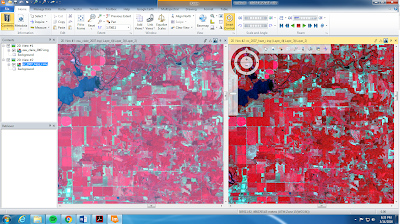
The next step was adding a viewer to the GCP window, which then added Spot Pan B to the Spot Pan imagery. Spot Pan was used as a reference for the Spot Pan B imagery. Another set of GCPs were collected to correct the second image, Spot Pan B (figure 10). After the regular GCPs were collected,
Automatic Tie Point Generation Properties feature was run. Tie points are points whose ground coordinates are unknown but are visually recognizable in the overlap areas between two or more images. The ouput
Auto Tie Summary was analyzed for accuracy. The accuracy was high so no further adjusting was needed.
 |
| Figure 10. GCP collection for Spot Pan B. |
The
Triangulation tool was then run using the
Iterations with Relaxation set at 3 and the
Image Coordinate Units for Report is set to
Pixels. Under the
Point tab, the
Same as Weighted Values type was selected and the X,Y, and Z values were all set to 15 meters (figure 11). The accuracy was measured and an output report was created which included the Root Mean Square Error.
 |
| Figure 11. Post triangulation. The triangles are GCPs and the squares are the tie points. The green and red rectangles at the bottom indicate how close the process of orthorectification is to being completed. |
The finishing touch of the lab was running the
Ortho Resampling Process. The DEM that was used previously was used as an input. The resampling that was selected was
Bilinear Interpolation. The second image was also added via the
Add Single Output window. And ta-da, there you have it, orthorectification!
Results:
To be able to see the anaglyphs in their full glory, you will need to use 3D glasses. The below anaglyphs produced very different output images. Through my eyes, the anaglyph created using the DEM (figure 12) was much more difficult to see the changes in 3D than in the DSM (figure 13). This is likely the case because the DSM had 2 meter resolution whereas the DEM had 10 meter resolution. I also believe this is because the DEM highlights smaller features such as buildings etc, whereas the DSM highlights larger surface features such as the elevation changes from terra_. The coloration of the images could also play a role in the extent of the ability to view the anaglyphs in 3D; the DSM is brighter and it is easier to tell without using the glasses that the imagery is supposed to be '3D'.
 |
| Figure 12. Anaglyph using DEM |
 |
| Figure 13. Anaglyph using DSM. |
The tedious process of using GCPs, tie points, triangulation, and the other functions to obtain the final output orthorectified image is complete (figure 14). The images overlap perfectly with each other to produce two images that are seamless (figure 15) and completely correct in it's X, Y, and Z coordinates.
 |
| Figure 14. Overlap of both orthographic pan images (Pan and PanB). |
|
|
Figure 15. This figure indicates the boundary (see diagonally) between the two orthographed images. Aside for the variation in brightness values, the images are matched up perfectly.
|
Conclusion:
There are quite a few ways in which there can be errors in imagery. It is important to take the time, as painstaking as it can be, to correct these errors in order to be able to properly analyze the images. Although this was a 'marathon' of a lab, I really liked having to use the GCPs to correct the images. Seeing 6 windows on the GCP Reference Source dialog can be extremely daunting, but I'm glad I was able to experience it by having well thought out directions before I get into the real world.
Sources:
National Agriculture Imagery Program (NAIP) images are from
United States Department of
Agriculture, 2005.
Digital Elevation Model (DEM) for Eau Claire, WI is from
United States Department of
Agriculture Natural Resources Conservation Service, 2010.
Lidar-derived surface model (DSM) for sections of Eau Claire and Chippewa are from Eau
Claire County and Chippewa County governments respectively.
Spot satellite images are from Erdas Imagine, 2009.
Digital elevation model (DEM) for Palm Spring, CA is from Erdas Imagine, 2009.
National Aerial Photography Program (NAPP) 2 meter images are from Erdas Imagine, 2009.